There's a lot to know regarding triangles on the ACT® Math Test. I'll keep the review of the theorems short since most students know them. If not, you can refer to Khan Academy or another source.
Beyond the foundational knowledge in area, perimeter and Pythagorean theorem, the ACT® Math frequently tests on special types of triangles, angles in triangles, and basic trigonometry. The last topic isn't very hard – so make sure you look at it at least once before you take your ACT®. Don't worry if you're not familiar with all of these - I'll cover what you need to know.
Basic Triangle Knowledge
- Area:
- Perimeter: The sum of all the sides
- Pythagorean Theorem:
Types of Triangles
Equilateral: all 3 sides of equal length
Isosceles: 2 sides of equal length
Right: 1 angle that equals 90 degrees
Similar Triangles
- AA = two angles are the same (this implies that the third angle is automatically equal, so all angles are equal).
- SAS = 2 sides are congruent and the angle between them is equal, then they are similar.
- SSS = all sides are proportional
Special Right Triangles
These are just special types of triangles known to mathematicians. These types also come up quite frequently on the ACT® Math Test. So if you know what these triangles are, then you'll be able to get some questions done a lot faster. If you don't know these, don't worry. You can usually figure out the properties of these special types of triangles by using the foundational knowledge above.
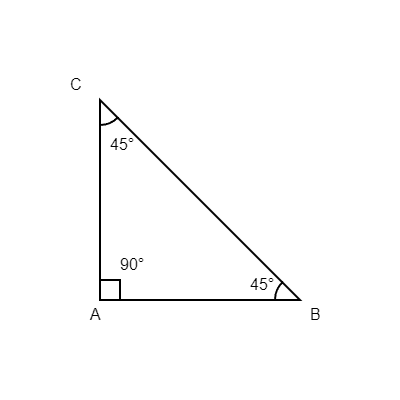
You need to know that there exists a category of triangles called 45 45 90 triangles. If one angle is 45 degrees and another is 90, then the remaining angle must be 45 degrees. This is a logical extension of the sum of the interior angles of a triangle, which we know must add up to 180 degrees.
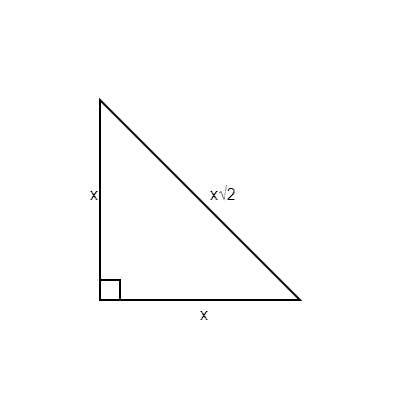
The is really an extension of the Pythagorean Theorem. Any triangle with two non-hypotenuse sides x and x will have hypotenuses of . You'll notice that this triangle always has interior angle measurements of 45, 45 and 90.
The ACT® Math Test commonly asks students to figure out the side lengths given the interior angle measurements. The only way to do this is by knowing the relationship between interior angle measurements and side lengths in special right triangles.
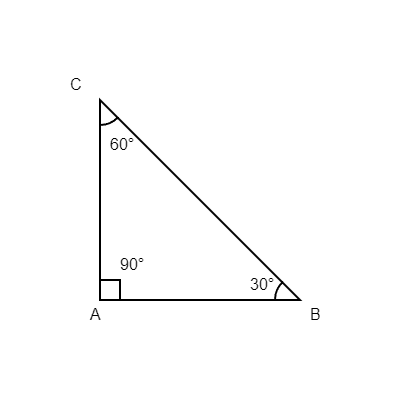
This type of triangle always has interior angle measurements of 30-60-90 degrees. If you see a triangle with 60 and 90 degrees, you can automatically deduce the missing angle will be 30 degrees.
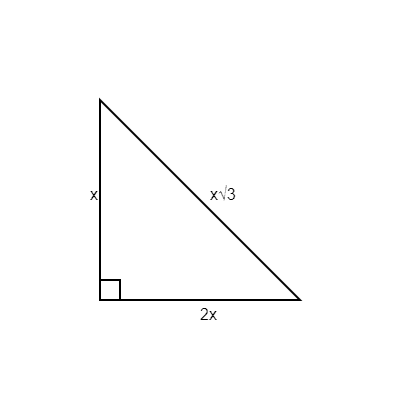
This type of triangle always has side lengths . We know to look for those side lengths when the ACT® Math Test gives us interior angle measurements of 30, 60, and 90, as in the triangle directly above.
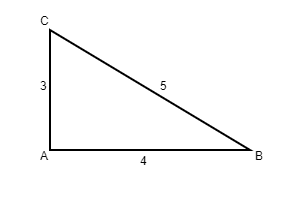
3-4-5 Triangle: This is a triangle that has the side lengths of 3, 4, and 5. This example is less important to know because you always figure out the side lengths using the Pythagorean Theorem. 3 4 5 Triangle show up quite frequently. Not necessarily as 3, 4 or 5, but as multiples in similar triangles, such as 6, 8 10; 12, 16, 20 and so on.
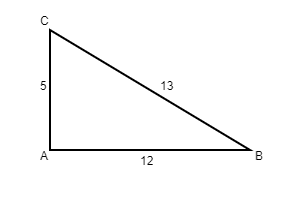
This is a triangle that has the side lengths of 5, 12, and 13. 5-12-13 Triangles are similar to 3-4-5 triangles in that their side lengths are proportional. You don't need to know this for the ACT®. But if you do recognize this relationship, you can solve some triangle questions more easily.
Angles in Triangles
We know that triangles have an interior measure equal to 180 degrees. So if we get a triangle with angles 72 and 48, we know the third angle must be:
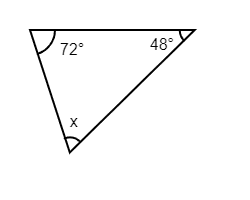
Click for the Answer
Given angles: $72^\circ and 48^\circ$ Sum of given angles: $120^\circ$ Third angle: $180^\circ - 120^\circ = 60^\circ$ The third angle in the triangle is $60^\circ$.
The ACT® Math Test can give you questions that are a bit harder, because they ask more complicated versions of the following.
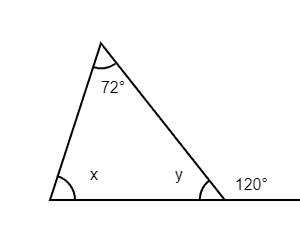
Let's say instead of 72, 48, and x, I told you triangle ABC has angles 72, x, and y, and that the angle BCD on the line = 120 degrees. Then what is angle x?
Click for the Answer
To solve for angle in the given triangle, we need to use the properties of angles in a triangle and the fact that the sum of angles on a straight line is .
Given:
- The triangle has angles , , and .
- The exterior angle on the line is .
1. Find angle using the straight line property: The sum of angles on a straight line is . Since the exterior angle is , angle can be
2. Use the sum of the interior angles of a triangle:
The sum of the interior angles of a triangle is . The triangle's angles are , (which we found to be ), and .
3. Set up the equation:
4. Solve for :
Angle is .
Beginners Trigonometry
The above topic says trig. If you haven't had precalc or never saw trig before, don't worry. The basic trig is very easy to comprehend. Take a few minutes to learn this or review it. Beginners trig is virtually guaranteed to show up, often multiple times per test.
SOHCAHTOA
The first thing you should associate with trigonometry is the mnemonic SOHCAHTOA. That helps you remember the following rules.
Sine: $Opposite\over Hypotenuse$
Cosine:$Adjacent \over Hypotenuse$
Tangent: $Opposite \over Adjacent$
The ACT® Math section frequently asks you to apply the basics of SOHCAHTOA. The best thing is, the test seldom makes you calculate the values for sine, cosine, or tangent. They just want you to find the numbers that, when solved, would give you any of those expressions. Keep reading to learn how.
Given triangle ABC, what is sin A? Recall that sine is always opposite/hypotenuse. The opposite will always be relative to the position of angle A. It is whatever side is opposite it and is also not the hypotenuse. So that leaves side AB. Then, hypotenuse is the longest side, CA. Therefore, for the purposes of the ACT® Math,$\sin A = AB \over CA$. That's all there is to it.
More Practice
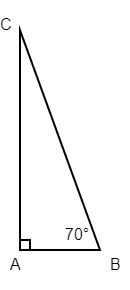
The way this can get more complicated is they could ask you something along the lines of what is the distance from AB of triangle ABC? The answer choices would include something along the lines of sin 70 CA. That's because $\sin 70 = AB \over CA$. So if we multiply both sides by CA, we would be left with $\sin 70 CA = AB$. AB still isn't a distance we can measure in real life, but it does satisfy the question.
How will this show up on the test?
Triangles show up on the ACT® Math Test in two ways. Either you'll get some straightforward application of basic geometry rules. These questions tend to occur only in the very beginning, 1-10, sometimes 1-20. More likely is that you'll have to figure out how to apply one of these triangle rules to another topic, usually algebra, to figure out an answer.