The Best ACT® Math Strategies: Tried and Tested

What are the best strategies for the Math on the ACT® Test? I’m an expert tutor with nearly a decade of experience helping high school students reach their dreams and increase their standardized test scores. These are the strategies I’ve proven have helped my students on the Math Test.

Read the Question

This is the first strategy a lot of students need. You might be reading this thinking, “really, dude? Read the question? That’s your strategy?” Yes. Yes, it is. Most students aren’t used to having to read questions that can sometimes be quite lengthy on a math test. That’s not usually the way you see questions in high school math class.

The ACT® Math Test will give you a lot of questions over the actual math problem it wants you to solve. You can seldom solve the problem without reading the question. Often, you’ll get the directions on what to do in the question. Other times, there will be information in the question you need to solve the problem.

If you don’t R.T.Q., you’ll be unable to solve a lot of the questions. Think about reading the question not as a waste of time, but a necessary step to earning the points you can already gain.

Process of Elimination

Process of Elimination has some good use cases on the ACT® Math Test. Sometimes when you get questions about definitions of numbers, shapes, or functions, POE can still be used even if you know the answer. A lot of students can use this method to check their work.

First, mark the answer choice you think is correct. Then, read the entire answer choice to prove each other one wrong. The ACT® Test loves making a wrong answer choice right up until the last ¼, where they add in some context that makes the answer entirely wrong. Remember, ¾ correct is still 100% wrong.

The other time Process of Elimination can help on the Math Test is when you truly do not know the answer to a question. Since the ACT® Test always pulls questions from cross-domains (for example, solve this geometry question using algebra) you’ll likely always know a part of the solution to a problem.

So if the question is asking which of the follow equations represents a circle, but you don’t know the equation of a circle, you can still use process of elimination. You probably know at least basic graphing. You can look at the equations and remove anything that seems entirely incorrect.

Consider this example

Which of the following equations represents the circle in the graph above?

1. A)
2. B)
3. C)
4. D)
5. E)

Let’s assume we know nothing about the standard form of a circle and try to solve this question using Process of Elimination. It’s hard to see how subtracting the x and Y parentheses would lead to a circle. It’d be like an inverse circle? (It’s actually a hyperbola.) So we can eliminate A and D. Physically cross them off.

We see from the graph that the circle is not at (0,0). It’s more in the bottom right quadrant. We can look at the values next to the xs and ys to see where the circle would end up if a given option were correct.

B)

• (x - 1)shifts 1 unit right, which matches the graph.

• (y + 2) is equivalent to (y - (-2)), which shifts 2 units down. This also matches the graph.

C)

• (x + 1) would shift left, which doesn't match the graph. Physically cross off the answer choice.

E)

• (x - 1) shifts right, which matches.

• (y - 2) would shift up, which doesn't match the graph. Physically cross off the answer choice.

Just by using process of elimination and our knowledge of graphs, we can come up with the right answer, B.

Plug in Answers

This strategy is kind of genius for the ACT® Math. You get to use the format of the standardized test against the ACT® Test… which is awesome. And they let you do this over and over again. Rather than bother solving potentially long math problems or perform a lot of steps, there are times you can simply evaluate the answer choices to see which is correct.

You can use this strategy on every test, multiple times. Even if you know how the math works on a given problem, you can still use this strategy to save a lot of time and prevent yourself from making a potential calculation error.

Let me explain with an example.

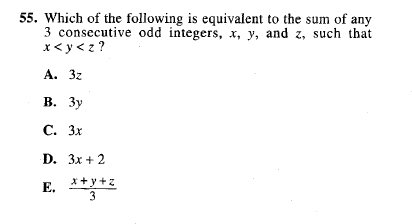
This question might seem hard because it’s #47 an also – what?! What kind of question is this? It’s not that bad, actually.

The ACT® Test has given you some random ‘D’ in the question and a bunch of random numbers in the answer choices. When this happens – when you have variables like D, x, y in the question and real numbers in the answer choices – you can plug in answers. One of them must be right. It’s a standardized test.

Let’s do just that. We’ll evaluate 2/D for D = 3, 4, 5, 7, 8, 9, and 16. To make this even easier, convert everything to decimals.

1/5 = 0.2 and 1/3 = 0.333

Which of these values lies between and ? 7, 8 and 9. Look at that – it corresponds exactly to answer choice D. That was easy, especially for such a high-level question.

Plug in Numbers

What about if the ACT® Math Test doesn’t give us real numbers in the answer choices, but just gives us variables everywhere? That may look overly complicated. But the solution to this type of question requires a level of abstraction just a little bit beyond Plugging in Answers.

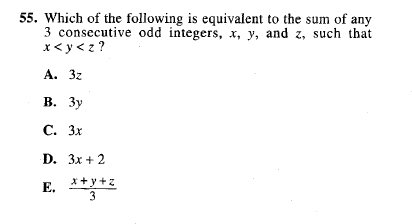
Instead, we’re going to sort of just make up random numbers and use then Plug In Numbers to solve the problem. The numbers are ones we pull out of the air. Don’t use 1 or negative numbers – they’ll give you some false positives where you think an answer is correct, when it isn’t. We’ll stick to nice easy numbers.

Then, we simply evaluate the answer choices for those numbers we randomly made up.

1. A)


2. B)


3. C)


4. D)


5. E)

Okay, that wasn’t so hard. But what is the question asking? Which of the following is equivalent to the sum of the three numbers? Oh, okay. What’s 3 + 5 + 7? 15. That corresponds to B! Which is the right answer.

Order of Difficulty

This is another helpful strategy for the ACT® Math Test. The questions get increasingly more difficult. For the ACT® Test, difficulty mostly means how many steps are required to solve a question. The problems in the beginning require few steps, whereas the problems towards the end require more steps. This introduces more places for students to make calculation errors.

If you’re struggling on the Math Test, focus on the lower numbered questions first. You don’t get more points for solving a harder question. All questions are worth the same number of total correct.

Also, don’t completely ignore the higher numbered questions. As you saw above, questions 47 and 55 above were actually pretty easy to solve. If you can recognize that, you can get those points easily.

There may be some questions towards the end where the Test is pulling from advanced topics in math. This is the other way that the ACT® Test means difficulty. If you don’t at least a 28, but more likely a 32+ on the Math Test, then I wouldn’t worry about the higher-level advanced concepts.

These concepts show up every once in a few decades. The ACT® Test has asked about natural logs (not regular logs) once and then never again. These concepts come up once and then are never seen again. You either know them or you don’t. Fortunately, this type of question is infrequent given the high frequency of other question types.

Scale is to Scale

If this doesn’t apply to you – great, move on and forget I ever brought it up. Some students read the directions at the top of the Math Test (yes, these exist). It says that not all figures may be drawn to scale.

This is just the ACT® Test’s disclaimer that if you were to bring a protractor to the Test and measure a given angle, it may not actually be 70 degrees all the way down to the hundredth of a thousandth of a percent. But it’s pretty close anyway, so you can reliably use the diagram to answer the question.

Scale is to scale. The Test almost never gives a diagram that isn’t to scale.