Stats Terms on the ACT® Math Test
Read time: 4 minutes Last updated: September 23rd, 2024
The ACT® Math Test includes several questions related to basic statistical terms such as mean, median, mode, and range. These questions can be straightforward, like calculating the mean of a set of numbers, or they might try to trick you, such as finding the range of an unsorted list. Let's look at these terms to help you achieve your highest score.
Defining Basic Terms
Mean is the average of a set of numbers.
Median is the middle value in an ordered list. If there's an odd number of values, it's the middle number. If there's an even number, it's the average of the two middle numbers.
Mode is the value that appears most frequently in a set of data.
Range is the difference between the largest and smallest values in a dataset.
Standard Deviation is a measure of how spread out the numbers are in a dataset. It tells us how much the data typically deviates from the mean.
When data follows a normal distribution (often called a bell curve), about 68% of the data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.
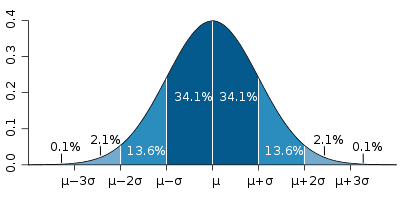
The ACT® Math Test usually asks about standard deviation in two ways:
- Understanding what the term means
- Knowing how data is distributed in terms of standard deviations from the mean
Fortunately, you won't need to calculate the standard deviation on the ACT® Math Test.
How Stats Terms Appear on the ACT® Math Test
Questions about statistical terms can appear in various forms on the ACT® Math Test. Here are some common types:
- Basic arithmetic to find mean, median, mode, or range
- Finding the median of an unsorted list
- Conceptual questions about what each term means
- Questions about data distribution within a given number of standard deviations from the mean (for standard deviation questions)
Practice Questions
Question 1:
What is the average test score?
Test Scores: 70, 85, 75, 90, 80, 100
- A) 83
- B) 80
- C) 85
- D) 75
- E) 90
Click for the Answer
Correct Answer: A) 83
Explanation:
Calculate the average: (70 + 85 + 75 + 90 + 80 + 100) ÷ 6 = 500 ÷ 6 = 83.33 (rounded to 83)
Question 2:
What is the mode?
Test Scores: 72, 85, 72, 90, 85, 72, 88, 85, 90, 85
- A) 85
- B) 72
- C) 90
- D) 88
- E) 80
Click for the Answer
Correct Answer: A. 85
Explanation:
The mode is the number that appears most frequently in the set: 72 appears 3 times 85 appears 4 times 90 appears 2 times 88 appears 1 time So, the mode is 85.
Question 3:
What is the median number of sales for the year?
Monthly Sales Values (in thousands):
| Month | Sales (in thousands) |
|---|---|
| January | 35 |
| February | 42 |
| March | 28 |
| April | 50 |
| May | 47 |
| June | 31 |
| July | 40 |
| August | 29 |
| September | 55 |
| October | 30 |
| November | 33 |
| December | 48 |
- A) 37.5
- B) 35
- C) 40
- D) 42
- E) 30
Click for the Answer
Correct Answer: A) 37.5
Explanation:
To find the median: 1. Order the values from smallest to largest: 28, 29, 30, 31, 33, 35, 40, 42, 47, 48, 50, 55 2. Since there are 12 values, the median will be the average of the 6th and 7th values: Median = (35 + 40) ÷ 2 = 37.5
Question 4:
4 people are sitting in a cafe. Their incomes are listed below. A millionaire with $1,000,000 walks in the door. Which is affected the most: the mean, the median, the mode, or the range?
Initial Earnings:
- Person 1: $30,000
- Person 2: $50,000
- Person 3: $75,000
- Person 4: $25,000
Click for the Answer
Correct Answer: The range is affected the most
Explanation:
Initial values: Mean: $45,000 Median: $40,000 Mode: No mode (all values unique) Range: $50,000 After millionaire enters: Mean: $236,000 (increase of $191,000) Median: $50,000 (increase of $10,000) Mode: Still no mode Range: $975,000 (increase of $925,000) The range is affected the most, increasing by $925,000.
Question 5:
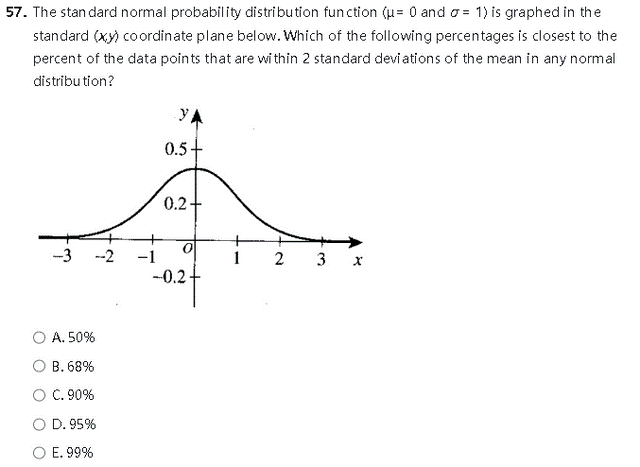
Click for the Answer
Correct Answer: D
Explanation:
Using the empirical rule, 95% of data falls within 2 standard deviations of the mean.
