The secret to understanding scientific notation for the ACT® is mastering exponent rules. Scientific notation is simply a way to express really big or really small numbers using exponents of ten.
Imagine you're a NASA scientist proposing different flight paths for a solar probe. You need to discuss various distances from the sun for potential observation points. The sun is 93,000,000 miles away. Without scientific notation, you'd have to say something along the lines of the following:
We could fly to point A which is 93,100,000 miles. We could go to Point B, which would save fuel at 92,900,000 miles away, but might damage the satellite. Or we could go to Point C, which is 93,500,000 miles away, where we might not get sufficient readings.
It's such a pain to read all of those numbers. Plus, you have to think a lot harder to compare the numbers. Consider this:
We could fly to point A which is 9.31 x 10⁷ miles. We could go to Point B, which would save fuel at 9.29 x 10⁷ miles away, but might damage the satellite. Or we could go to Point C, which is 9.35 x 10⁷ miles away, where we might not get sufficient readings.
At a glance, we can easily compare 9.31, 9.29, and 9.35. That's why scientific notation can be useful when talking about large numbers.
How's this going to show up on the ACT® Math Section?
The ACT® Math likes to use scientific notation to test exponent rules. The test will typically give both the question and the answer choices in scientific notation. You need to know what scientific notation is. Once you know that, the questions are really asking about exponent rules.
Here's a helpful hint: When you see scientific notation on the ACT®, you can often solve the problem by focusing on the exponents. You don't always need to calculate the entire number.
Let's look at a typical ACT® question involving scientific notation and astronomical distances:
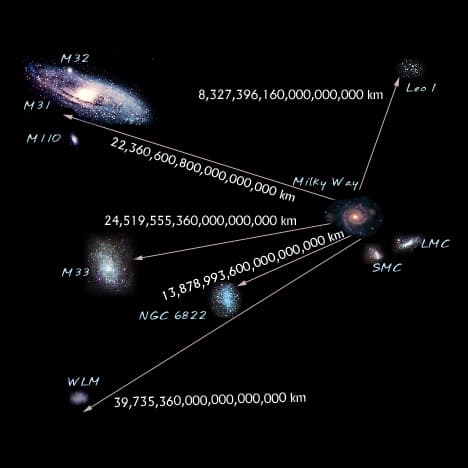
Question:
Distance AB is the distance from the Milky Way to M33 is 2.451 x 10¹⁹ miles. Distance AC is the distance from the Milky Way to WLM is 3.973 x 10¹⁹ miles. How many times longer is Distance AB than Distance AC?
- 0.6
- 1.6
- 2.6
- 3.6
- 4.6
Click for the Answer
Correct Answer: B. 1.6
Explanation:
The correct answer is found by dividing the distances: (2.451 x 10¹⁹) / (3.973 x 10¹⁹) ≈ 0.616, which rounds to 1.6.
Source No changes made
This question tests your understanding of scientific notation and your ability to perform calculations with very small numbers.
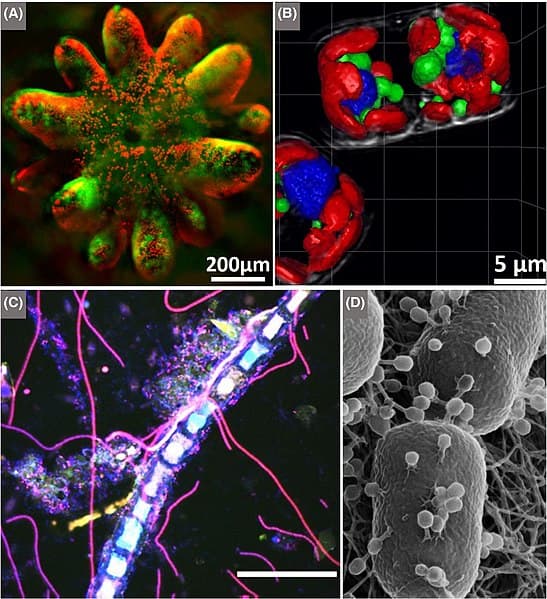
Picture A is a coral polyp. Its size is recorded as 200 µm, or 2.0 x 10⁻⁴ meters.
Picture B is a fluorescence micrograph of the diatom Thalassiosira nanae (a type of phytoplankton). Its size is 5 µm, or 5 x 10⁻⁶ meters.
One micrometer is expressed as 1 micrometer (µm) = 10⁻⁶ meters.
Question:
Which of the following would express the number of Thalassiosira nanae that would fit inside one coral polyp, in scientific notation?
- 4.0 × 10⁻¹
- (5 × 10⁻⁶) / (2.0 × 10⁻⁴)
- (2.0 × 10⁻⁴) / (5 × 10⁻⁶)
- 4.0 × 10²
- 4.0 × 10⁻²
Click for the Answer
Correct Answer: D. 4.0 × 10²
Explanation:
Remember, when dividing numbers in scientific notation, you subtract the exponents. This is a concept that the ACT® often tests.
(2.0 × 10⁻⁴ meters) / (5 × 10⁻⁶ meters) = 4.0 × 10²
You may have known that the answer to this question was 40 from the start. This is a good example of how the ACT® Math sometimes is more concerned with the correct application of exponent rules and scientific notation.