Quadrilaterals are a common topic on the ACT® Math Test. While you might already know the basics, applying these rules in different contexts can be challenging. Let's look at what you need to know.
All quadrilaterals have interior angles that add up to 360 degrees. This fact is your starting point when the ACT® Math asks you to find a missing angle. From there, you'll need to use the given information to figure out the unknown angle(s).
Basic Formulas
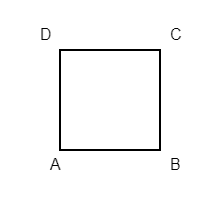
Square
- Area:
- Perimeter:
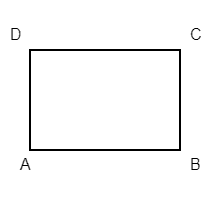
Rectangle
- Area:
- Perimeter:
The ACT® Math often includes questions about more complex quadrilaterals, particularly parallelograms and trapezoids. Let's look at each of these in more detail.
Parallelogram
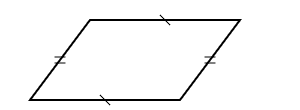
A parallelogram has two pairs of parallel sides. It can look like a square (all four sides equal) or a rectangle (two pairs of equal sides). When all sides of a parallelogram are equal, it's called a rhombus. All rhombuses are parallelograms, but not all parallelograms are rhombuses.
The ACT® Math frequently asks about the interior angles of parallelograms. Keep in mind that opposite angles in a parallelogram are always equal. Let's look at an example:
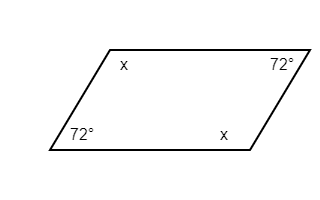
What would x be?
Click for the Answer
To find x in this parallelogram, you can use the fact that all angles add up to 360 degrees:
You start by setting the equation equal to 360 degrees (the sum of interior angles in any quadrilateral). Then, you identify the known angles (72 and 72) and represent the unknown angles with x.
Trapezoids
While trapezoid questions are less common, they often combine rectangles and triangles. There's a specific formula for trapezoid area (A = (a+b)/2 × h), but it's more useful to understand how shapes within a trapezoid work.
Example Problem
Let's look at an example from a real ACT® Test:
This question asks for the area of two combined triangles within a trapezoid. The trapezoid has a total base of 8 inches, with a 4-inch rectangle in the middle. This leaves 4 inches split between two triangles, so each triangle has a 2-inch base.
To find the area of both triangles, you can use the formula A = 1/2bh. Since there are two triangles, you can simplify this to just bh. With a base of 2 inches and a height of 3 inches for each triangle, the total area is 2 × 3 = 6 square inches.
Even if the image doesn't look perfectly to scale, trust the given measurements and apply your knowledge of quadrilateral properties.
Conclusion
Understanding these quadrilateral concepts and practicing their application will help you tackle similar questions on the ACT® Math Test.