Other Polygons
The ACT® Math Test asks about other polygons besides triangles and quadrilaterals in two main ways. The first is by asking about a certain shape. They may tell you that there is a heptagon without showing you what a heptagon is.
Here's a reference list:
- 3 tri
- 4 tetra (quad in Latin)
- 5 penta
- 6 hexa
- 7 hepta
- 8 octo
Then, they can ask any number of questions based on the above information.
The second thing that's important for the ACT® Math is the number of interior angles. You can calculate this by adding 180 degrees for every angle past 3. This makes sense if you think about the difference between a triangle and a square. A triangle has 180 degrees and 3 angles. A square has 360 degrees and 4 angles.
Cosnider This Example
If you have a pentagon (5 sides), you'd calculate:
(5 - 3) * 180 = 2 * 180 = 360 degrees
So a pentagon has 540 degrees total for its interior angles.
There is also an explicit formula some students find easier to remember. That's (n-2) × 180, where n is the number of sides. So a quadrilateral has 4 sides. That 4-2 × 180 = 360. You can do that for any polygon of any number of sides.
Once you understand how to find the degrees in any given polygon, you'll be able to proceed to the next steps for any given polygon question on the ACT® Math Test. There's no one common question that you'll receive to test you on this concept. Instead, the questions tend to be quite different every time. The only similarity is the expectation that you'll be able to find the total number of degrees of the interior angles.
Volume
Volume is important, just remember to find the area and then height.
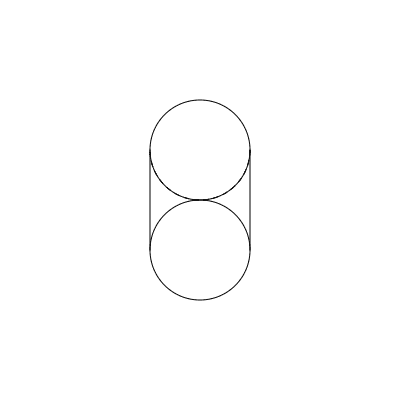
Let's say the area of a circle is πr². That would give us the area for the bottom of the cylinder. Then, if I want to find the volume, I just multiply by the height.
For cubes, it's the same thing. Find the area of a square, s². Then multiply by the height – which is the same thing.
There are explicit formulas for these concepts. I find that students have an easier time remembering how to find volume when it's explained in this way.
Dilations
Dilations in geometry refer to enlarging or shrinking a shape while maintaining its proportions. On the ACT® Math Test, this concept often appears in word problems where you need to figure out how to use words and ratios together to solve problems on shapes.
Let's say you have the circle above. It has a diameter of 1 foot. You're going to increase the diameter by 75%. What is the new diameter?
Click for the Answer
Some students might say 0.75. It's actually 1.75. That's because the ACT® Math wants to make sure you can reason from geometry to correctly apply percentage and other rules.
Dilations questions involve an increase in some size on the shape. Then you will have to answer how much a part or the whole of the shape increased. If you apply the geometry rules regarding the sizes of shapes and their volume, you should be able to extend that knowledge to these questions.