Piecewise Functions on the ACT® Math
Read time: 5 minutes Last updated: September 23rd, 2024
What a name! Fortunately, it's not as hard to understand as it is to say. A piecewise (or piecewise-defined) function is simply a function that's defined differently for different parts of its domain. In other words, the function follows one rule for some input values and different rules for others.
We encounter piecewise functions more often than you might think. One everyday example is the U.S. tax code. Let's take a closer look:
Consider this example
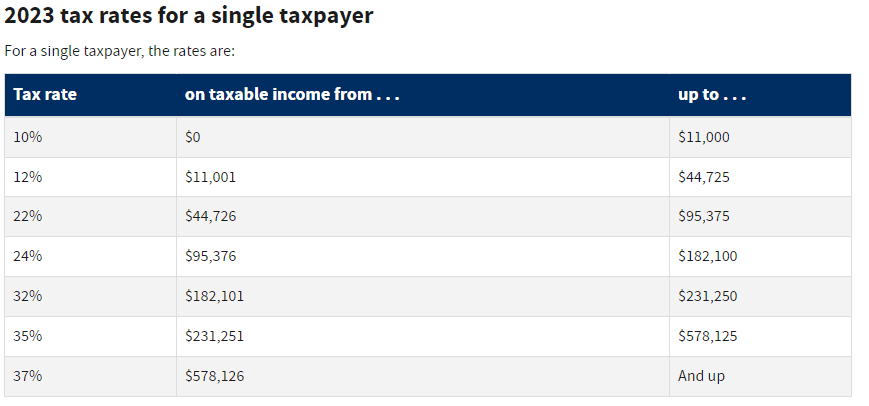
Consider this simplified tax rate structure:
For
,
For
,
For
,
Let's say you make $50,000. How much is your federal tax?
To solve this, we need to use the third piece of the function because $50,000 falls in the range of $44,726 to $95,375.
Tax = 5,147.12 + 0.22(50,000 - 44,726)
= 5,147.12 + 0.22(5,274)
= 5,147.12 + 1,160.28
= 6,307.40
So, the federal tax on a $50,000 income would be $6,307.40.
How will this show up on the ACT®?
The ACT® Math section may not explicitly use the term "piecewise function." Instead, you'll likely see questions that provide different equations for different value ranges. The test wants to see if you can:
- Read and understand that you need to use different functions based on the given value.
- Choose the correct piece of the function to use.
- Accurately perform the required calculations.
If you can do these three things, you'll be in good shape to tackle piecewise function questions on the ACT®.
Practice Section
Let's work through some practice questions to help you get comfortable with piecewise functions.
Question 1:
Evaluate the piecewise function at
f(x) =
For
,
For
,
For
,
- A) 25
- B) 10
- C) 15
- D) 5
- E) 3
Click for the Answer
Correct Answer: A. 25
Explanation:
To solve this, first identify which piece of the function to use. Since x = 5, and , we use the second piece: .
So, f(5) =
Question 2:
Evaluate the piecewise function at
(Using the same function as Question 1)
- A) -3
- B) 1
- C) 3
- D) -1
- E) 0
Click for the Answer
Correct Answer: A. -3
Explanation:
For x = -3, we use the first piece of the function because .
f(-3) = 2(-3) + 3 = -6 + 3 = -3
Question 3:
Evaluate the piecewise function at
(Using the same function as Questions 1 and 2)
- A) -5
- B) -7
- C) -9
- D) -11
- E) -13
Click for the Answer
Correct Answer: A. -5
Explanation:
For x = 12, we use the third piece of the function because .
f(12) = -12 + 7 = -5
Key Takeaways
- Piecewise functions use different rules for different input values.
- Always check which piece of the function applies to your given x-value.
- Once you've identified the correct piece, solve it like any other function.
- Practice reading and interpreting piecewise functions to improve your speed and accuracy on the ACT®.
Conclusion
Remember, piecewise functions might seem tricky at first, but with practice, you'll find they're just a matter of choosing the right piece and solving as usual.
