Complete Guide to Angles: ACT® Math 2024

Angle measurement problems appear often on the ACT® Math section. There are two key things to understand: the angle measurement theorems (don't worry, there aren't many) and how to apply them. The ACT® Math section will often give you different algebra problems with these problems.

Although you don't need to memorize angle names for the ACT Math® section, knowing them can help you understand how angles work.

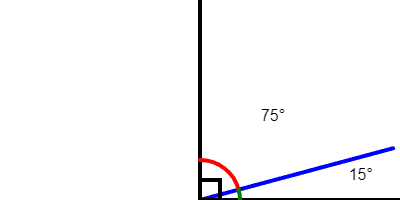
Complementary angles * add up to 90 degrees. They're formed when two lines meet at a right angle from the same point. On the ACT Math®, complementary angles are usually marked with a right angle symbol, unless you're asked to figure out if an angle is 90 degrees or complementary.

* Not to be confused with complimentary, which is when something suits you. Complement = complete; compliment = you look nice!

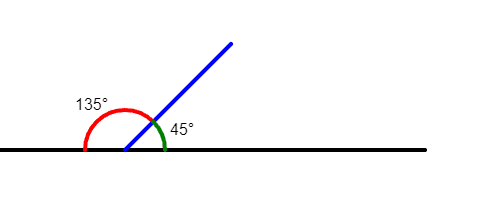
Supplementary angles add up to 180 degrees - the same as a straight line. If you draw an angle from one point on a straight line to another, it forms a semi-circle or 180-degree line.

If you keep going all the way around to where you started, you'd make a full circle of 360 degrees.

A straight line has supplementary angles on both sides, totaling 360 degrees. That's 180 on top and 180 on bottom, or 180 on the left and 180 on the right if you split it vertically.

Angles of Different Types of Lines

Different types of lines create different types of angles.

Perpendicular lines intersect at 90-degree angles, forming 2 pairs of complementary angles, or 4 equal angles.

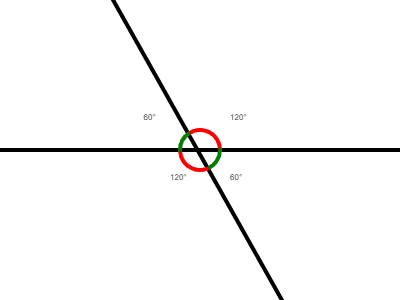
Two intersecting lines form opposite angles. Opposite angles are always equivalent. We know the total number of degrees in a line. Intersecting a line with another line can only create 2 pairs of equal opposite angles.

Parallel lines never intersect. They run along forever without ever touching once. They don't form angles by themselves, but when they are intersected by a line (the technical math term for this is a transversal, which isn't important for the test itself), the parallel lines form opposite interior angles. The ACT® Math section likes to test on opposite interior angles.

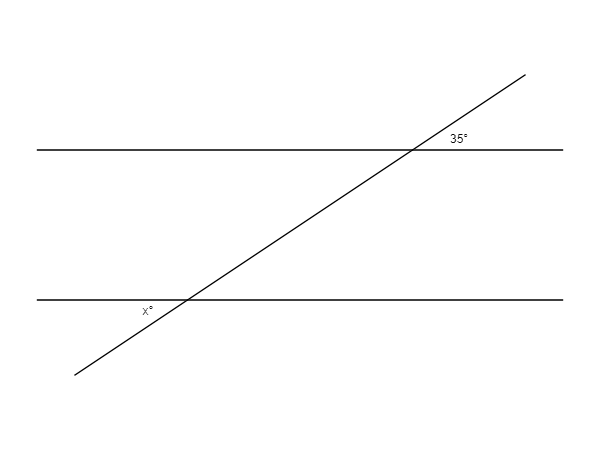
Question 2:

Two parallel lines above intersect. What is the measurement of angle ?

Answer Choices:

1. A) degrees
2. B) degrees
3. C) degrees
4. D) degrees
5. E) degrees

Click for the Answer

Correct Answer: A) degrees

Explanation:

Correct. The straight line has 180 degrees. So we use algebra to solve: , then the angle to the left of 50 must be degrees. Since the opposite angles are equal, degrees.

• B) degrees - Incorrect. This value is higher than the correct value by 10 degrees.
• C) degrees - Incorrect. This value is lower than the correct value by 10 degrees.
• D) degrees - Incorrect. This value is higher than the correct value by 20 degrees.
• E) degrees - Incorrect. This value is higher than the correct value by 30 degrees.

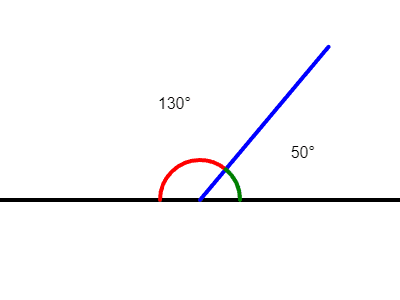
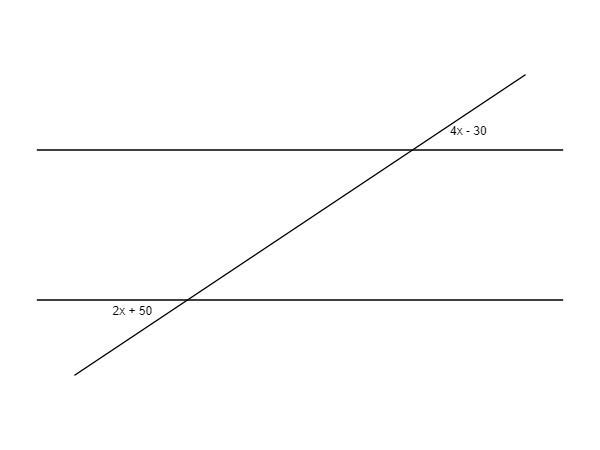
Question 3:

Two parallel lines intersected by a transversal create an angle of degrees on one side of the transversal and degrees on the other side. What is the value of ?

Answer Choices:

1. A)
2. B)
3. C)
4. D)
5. E)

Click for the Answer

Correct Answer: C)

Explanation:

Correct. The angles are supplementary because they form a straight line. So, . Simplifying, . Solving for , and .

• A) - Incorrect. This value does not satisfy the equation .
• B) - Incorrect. This value does not satisfy the equation .
• D) - Incorrect. This value does not satisfy the equation .
• E) - Incorrect. This value does not satisfy the equation .

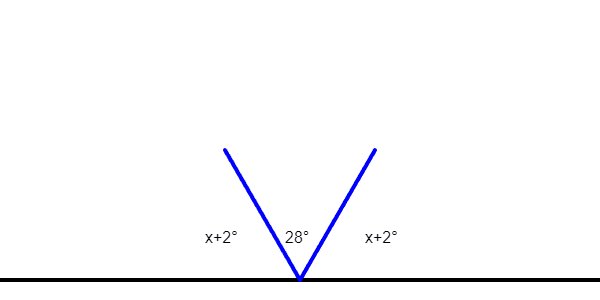
Question 4:

A straight line has three angles: , 28, and . What is ?

Answer Choices:

1. A) 24
2. B) 26
3. C) 25
4. D) 27
5. E) 30

Click for the Answer

Correct Answer: C) 25

Explanation:

Correct. Substituting into gives 27. Summing the angles: , which equals 180.

• A) 24 - Incorrect. Substituting into gives 26. Summing the angles: , which does not equal 180.
• B) 26 - Incorrect. Substituting into gives 28. Summing the angles: , which does not equal 180.
• D) 27 - Incorrect. Substituting into gives 29. Summing the angles: , which does not equal 180.
• E) 30 - Incorrect. Substituting into gives 32. Summing the angles: , which does not equal 180.