Advanced Trig Made Easy for the ACT® Math
Read time: 3 minutes 30 seconds Last updated: September 23rd, 2024
Advanced trigonometry is a crucial topic on the ACT® Math section. While it may seem intimidating at first, understanding these concepts can improve your score by several .
This guide will walk you through the Law of Sines and Cosines, two important trigonometric principles that often appear on the Test.
Law of Sines and Cosines
You don't necessarily need to remember the explicit formulas for the Law of Sines and Cosines since they are almost always provided on the test.
However, they're not always given. The most important thing to remember is when to use each, then the exact way to apply each formula.
Law of Sines
The Law of Sines is expressed as:
= =
While the Law of Sines is less frequently tested, it does appear from time to time. The ACT® Math section seldom requires you to work with actual numbers. Instead, the test usually wants to see if you can apply the basic principles of the Law.
Let's look at an example typical of the Law of Sines questions on the ACT® Math:
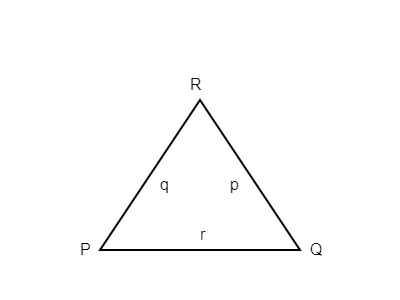
This diagram illustrates a practical application of the Law of Sines in engineering. It shows a valley with points P, Q, and R, representing the problem we'll solve below.
Problem:
An engineer needs to find the distance from point P to point R across a valley as shown in the figure above. The measurements of which of the following angles and side lengths are sufficient for the engineer to determine the length of PR using only the law of sines?
Note: The law of sines states
=
=
Using the law of sines:
=
=
To find
in terms of
and
:
=
Solving for
:
=
Answer Choices:
- A) Angles P, Q and side length p
- B) Angle P and side length r
- C) Angle Q and side lengths p, r
- D) Angle Q and side length r
- E) Angle R and side length p
Click for the Answer
Correct Answer: A) Angles P, Q and side length p
Explanation:
This choice provides two angles and one side length. Using the law of sines, knowing two angles and one side length allows the calculation of the third angle (R) and the remaining sides (q and r).
Law of Cosines
The Law of Cosines is expressed as:
The Law of Cosines appears much more frequently than the Law of Sines on the ACT®. The formula is usually, but not always, provided with the question on the test. To apply the formula effectively, make sure you read the question carefully, figure out what it's asking, and then solve as many pieces as you can with the given information.
Let's look at an example of how the Law of Cosines might appear on the ACT®:
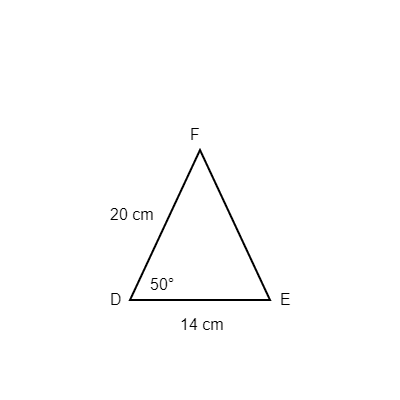
This diagram shows Triangle DEF, which we'll use to solve the problem below using the Law of Cosines.
Problem:
Triangle △DEF is shown in the figure above. The measure of ∠D is 50∘, DE=14 cm, and DF=20 cm. Which of the following is the length, in centimeters, of EF?
Note: For a triangle with sides of length a, b, and c opposite angles A, B, and C, respectively, the law of cosines states
.
Answer Choices:
- A) 14 * sin 50∘
- B) 20 * sin 50∘
- C)
- D)
- E)
Click for the Answer
Correct Answer: E)
Explanation:
This is the correct application of the law of cosines to solve for the length of EF.
How Advanced Trigonometry Appears on the ACT® Math Test
In my experience, the ACT® Math section rarely requires you to solve these equations for real numbers. Usually, correctly placing all the numbers in the right spots in the formula is sufficient to earn full points. The test typically asks you to determine which law is appropriate to use, then how to correctly fill in the a, b, and c values.
If you can do that, you'll likely get the question correct. The answer choices will almost always be formulas with real values plugged in, but not solved.
